Waves#
What you need to know
A wave is a self-propagating disturbance in a medium. Waves carry energy, momentum, information, but not matter!
The wave equation, a partial differential equation (PDE), completely describes waves’ spatial and temporal evolution.
Waves can be standing or travelling. Transverse or longitudinal.
Waves, waves and more waves#
Sound Waves.
Waves on a guitar string.
Waves on the surface of the water.
Quantum mechanical waves. E.g electron waves, neutron waves, hydrogen waves, etc.
Electromagnetic waves (e.g. light, UV, X-rays) – this is the only kind of wave which does not require a medium! EM waves can travel in vacuum. In a sense, an EM wave “rolls out its own carpet” hence creating its own medium as it moves forward.
Gravitational waves traveling through spacetime
Classification of waves by orientation: Transverse vs Longitudinal#

Classification of waves by appearance: Standing vs Traveling#
Traveling waves move with respect to fixed reference frame.
Standing waves move in place.
Defining wave mathematically#
Since wave is a moving disturbance \(u\), we describe this disturbance (e.g. vertical displacement) by specifying change of disturbance as a function of space \(x\) and time \(t\) via: \(u(x,t) = f(x, t)\).
Imagine an ocean wave. For an observer standing on a wave (surfer) the wave stands still but for the observer standing on the shore the wave moves away with velocity: \(x'=x-vt\)
Assuming that shape of the wave stays the same we can express the motion of wave in the reference frame of the still observer: \(f(x,t)=f(x')\)
Traveling waves.#
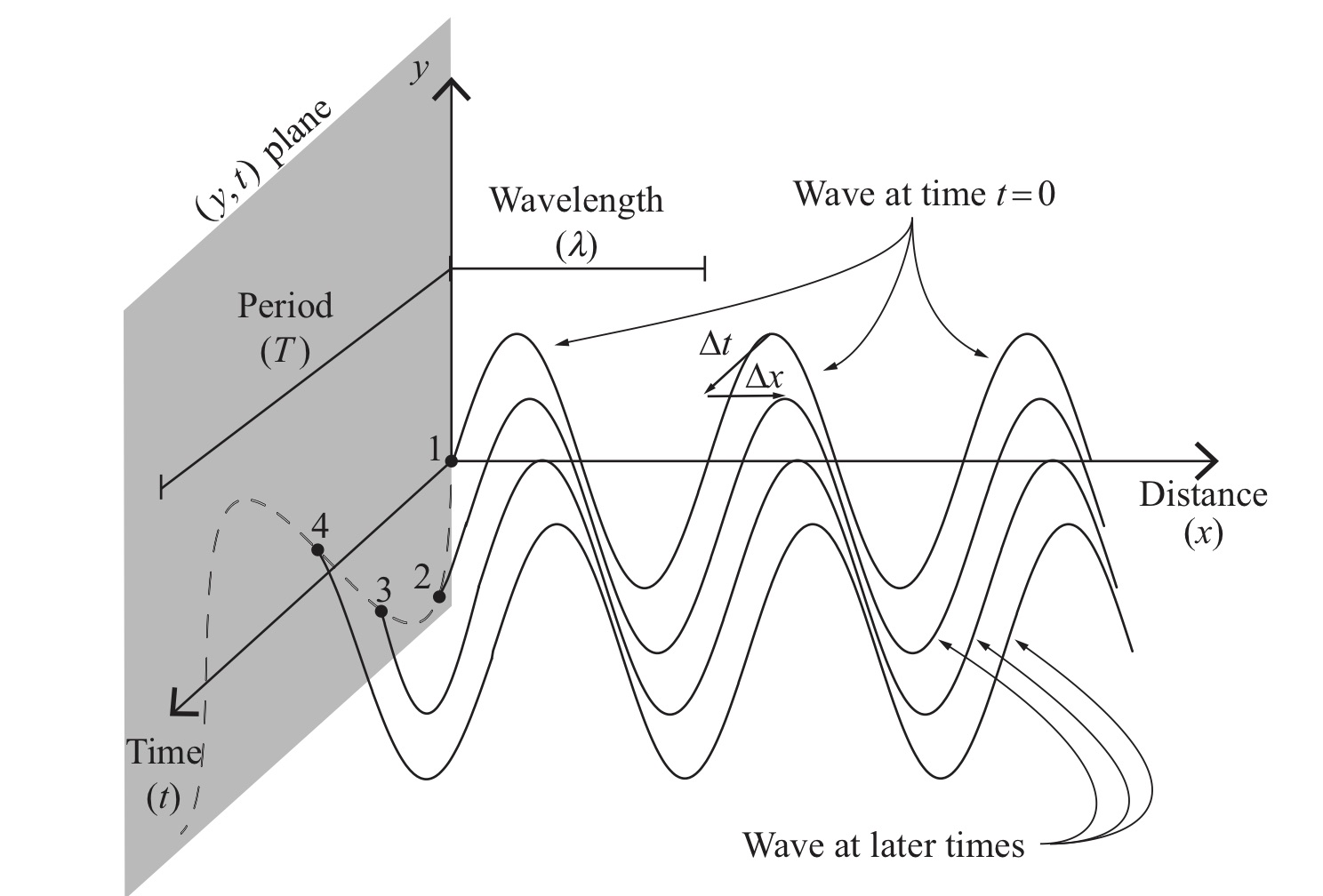
We will be working a lot with periodic waves that have a shape of a sine or cosine, like this one: $\(y(x,t)= A \sin(kx)\)\( Let us now turn this sinusoidal form into a wave traveling along x axis: \)\(y(x,t)= A \sin(k(x-vt))=A \sin(kx-\omega t)\)$
Amplitude \(A\): specifies maximum disturbance.
Wave number \(k\): specifies periodicity in space.
Angular frequency \(\omega\): specifies periodicity in time.
Flashback to first lecture when we had this relationship of wavelength to speed of wave and frequency via \(\lambda \nu = v\) and \(\nu=\frac{1}{T}\)
Wave equation.#
We obtain equation of motion by using the chain rule and taking partial derivatives of \(u\) with respect to \(x\) and \(t\).
Just as in classical mechanics we need to take second derivative in order to get the equation of motion that is determined by initial position and velocity. By using the chain rule and taking one more derivative with respect to \(x\) and \(t\) we obtain:
We just obtained a 1D classical wave equation. Solutions of this equation are functions of time and space called wave functions.
Wave interference: definition#
Interference – a phenomenon of combining waves which results in a new wave of greater, lower, or the same amplitude.
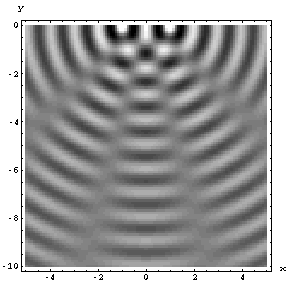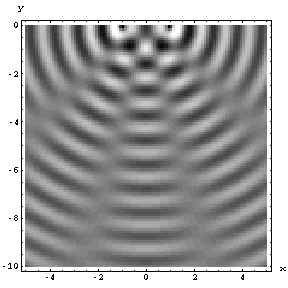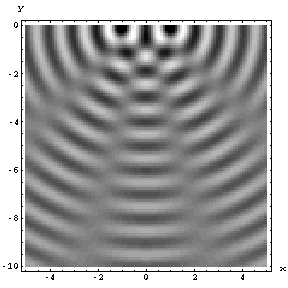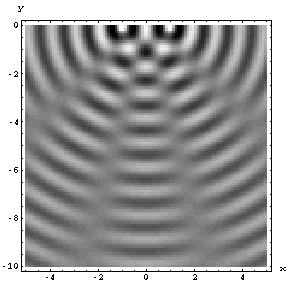
This follows from the superposition principle to which we will be returning many times later in the class. The principle of superposition states that if waves \(A\) and \(B\) are both solutions of the wave equation, then so is a wave \(C = A + B\).
Wave interference: derivation.#
Considering two sinusoidal waves of the same amplitude, wavelength, and direction of propagation but with a slight different phase \(\phi\) (e.g sound waves of a song coming from different holes on a wall). The resultant wave would be:
If we sum up the two phase-shifted waves and make use of trigonometric relation:
we get:
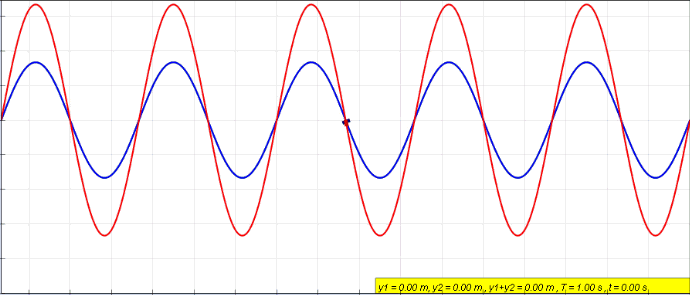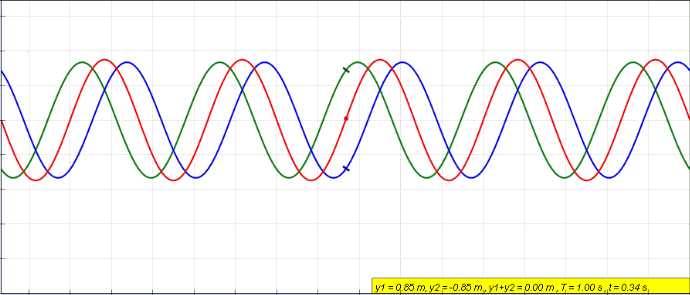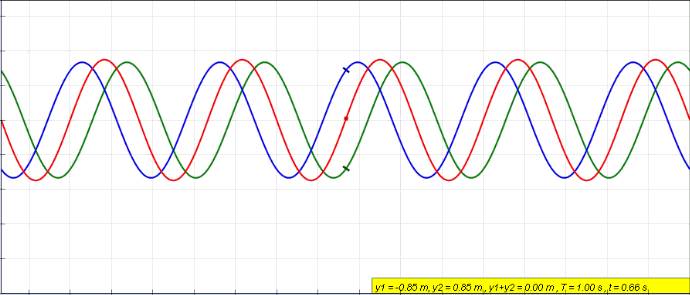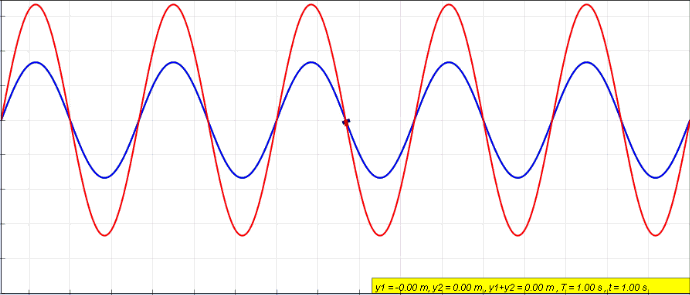
Wave interference: demonstration.#
When two waves interfere, their amplitude can double (constructive interference) become 0 (destructive interference) or anything in between:
\(\phi=0\) Fully constructive interference \(y(x,t)=2A \cos(kx-\omega t)\)
\(\phi=\pi\) Fully destructive interference. \(y(x,t)=0\)