The need for quantization#
What you need to know
Energies of atoms, molecules and light are quantized. Quantized means that energies assuming strictly defined discrete values as opposed to having continuum range.
Quantization of energy is a fundamental aspect of our physical reality and is observed in all quantum experiments. Quantum mechanics provies thorough explanation and prediction of quantization.
Key historical developments leading to the birth of QM are black body radiation, double slit experiment, photoelectric effect
Some macroscopic phenomena, such as the red color of hot metals, heat capacity of solids at a low temperature, and colors of matter are all due to quantum effects.
What is the nature of light?#
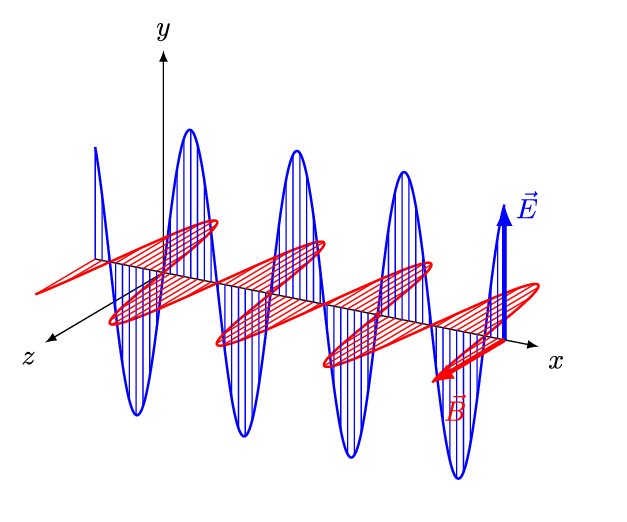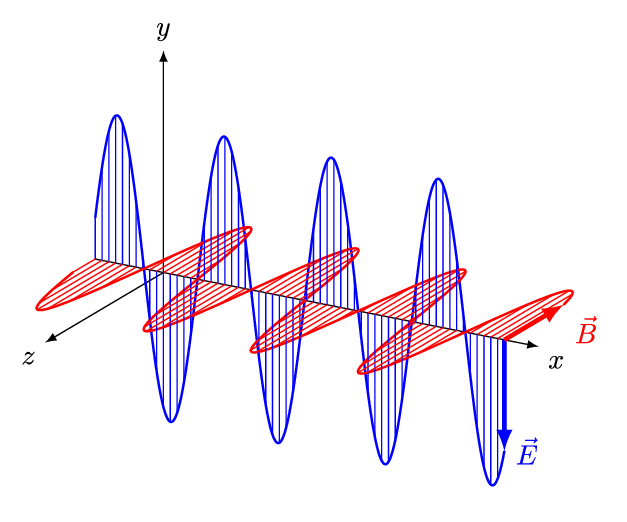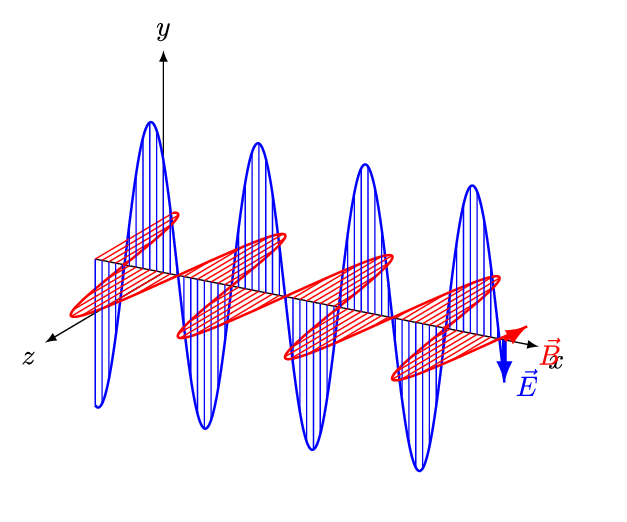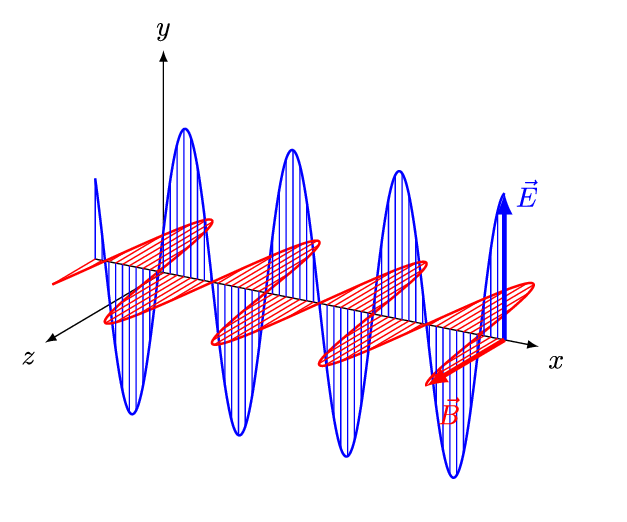
According to the classical wave theory light is seen as a traveling wave consisting of electric and magnetic components.
We will soon see that this picture of light as enelectromagnetic wave is not the whole story and radically new ideas are needed to understand wide variety of phenomena invlving interaction of light with atoms and molecules.
Spectrum of electromagnetic waves#
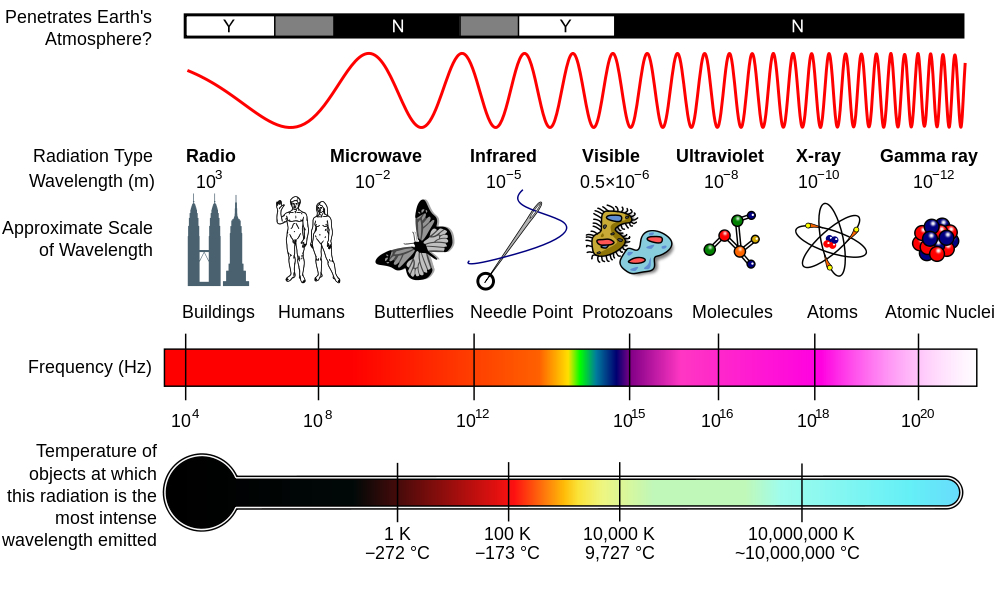
High-frequency waves carry much higher energy. This means X-ray or Gamma-rays can only be generated by heating “stuff” up at very high temperatures. This happens naturally at the core of the sun!
Low-frequency waves carry less energy. Can be generated in a “microwave” or by broadcasting antennas.
The visible light. occupies a narrow frequency region in between.
Relationship between frequency, wavelength and speed of light.#
Wavelength \(\lambda\) and frequency \(\nu\) of light are inversely proportional with constant of proportionality being the speed of light c:
Think of wavelength as distance between wave peaks (nanometers, nm)
Think of frequency as a distance traveled in 1 second (hz).
Speed of light in vacuum, c is a constant (\(3 \cdot 10^8 m/s\)). Thus knowing the wavelength allows you to compute the frequency and vice versa.
What is the relationship between frequency of radiation \(\nu\) and energy \(E\)?#
This is not such a trivial question. In fact, this very question arose in connection with black body radiation; an experiment that forever changed the course of history by giving birth to quantum mechanics!
Black body as a model for all radiating objects.#

Thermodynamically speaking.#
A black body is an idealized system which is in equilibrium, maintained at some constant Temperature T which both absorbs and emits every wavelength of electromagnetic radiation
Equilibrium condition in thermodynamics means that the system emits as much energy as it absorbs. In other words outflux = influx.
The reason its called black body is that it absorbs every wavelength that hits the surface, therefore, appearing as 100% perfect black object.
If an object has a color, it is because it is reflecting certain wavelengths of light which then gets detected by our eye retina. The distribution of wavelengths, which is emitted by a blackbody, is determined only by its temperature!
Applications of black Body radiation#
The black body is used as a standard with which the absorption of real bodies is compared. To a good approximation, stars radiate like blackbody radiators. Thus we can use blackbody radiation as a model to infer the temperature of the stars from their colors!
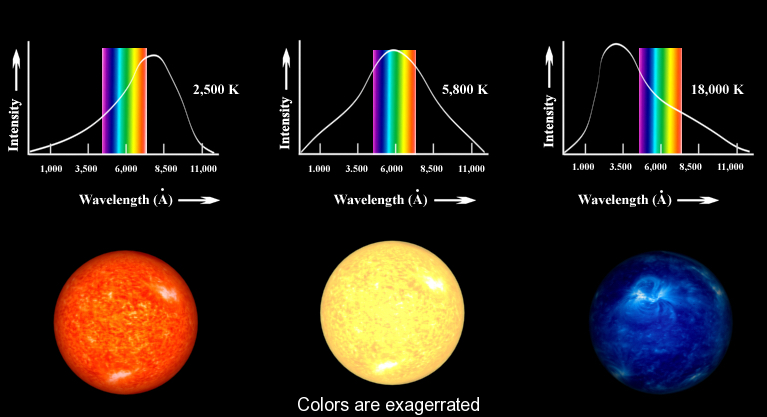
Key features of black body radiation?#
As temperature T goes up we notice three things:
Radiation intensity goes up, implying higher radiation energy.
Distribution of wavelengths shifts left to lower values (left panel) or we can say the distribution of frequency shifts right (right panel)
Color of the object changes from red to yellow to blue.
What is classical mechanics & thermodynamics perspective on black body radiation?#
What is “temperature”? A measure for kinetic energy per particle associated with translational, rotational, vibrational degrees of freedom.
What is light? Think of an oscillating spring with frequency \(\nu\)
Thermodynamics: Heat can only flow from high to low temperature. In equilibrium, each degree of freedom in our case each spring/oscillator gets the same thermal energy \(k_B T\).
Implications of classical mechanics.#
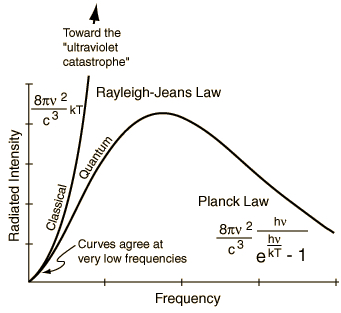
Classical mechanics reasoning about black body radiation goes like this:
One can fit more of high fequency (short wavelength) waves in the box than small frequency ones. The number of waves with small frequency region \([\nu, \nu+d\nu]\) is:
From thermodynamics we know that in equilibrium each degree of freedom or each oscillator gets the same \(k_BT\) of energy.
Thus the energy distribution of radiation is:
Energy distribution shoots to infinity at high \(\nu\) (or low \(\lambda\)). This is known as the ultraviolet catastrophe!
Quiz
What is the problem with classical mechanical explanation of black body radiation?
It is not corectly applied.
CM makes some uncontrolled approximations about energy.
CM can not model waves.
Classical mechanics does not have a way to account for the quantization of energy.
Max Planck and the trick of quantization#
In 1900 Planck found that the theoretical curve can very closely match the experimental curve if one postulates that only discrete (quantized) values of energy are possible.
Plack equation
Unit of planck constant, \(h = 6.63 10^{–34} J s\)
Unit of frequency \(\nu\), \(s^{-1}\).
This means atoms and molecules absorb and emit radiation in discrete quantities, multiples of \(h\nu\), which are called quanta! \(E_1, E_2,E_3 …\)
When light is emitted or absorbed, the atom or molecule jumps from one state to another and the energy difference \(h\nu = E_n - E_m\) is either coming from light or is used to generate light.
Note how small \(h\) is in the macroscopic units (such as J s). This is why quantization of energy is hardly noticeable and classical mechanics works so well at the macro scale. In the limit \(h \rightarrow 0\), \(E\) becomes continuous, and an arbitrary real value of E is allowed. This is the classical limit.
The black body radiation distribution function#
assuming that the energy of an oscillator is quantized, Planck showed that the cor- rect thermodynamic relation for the average energy is
Instead of uniform value \(kT\) given by classical mechanics we end up with distirbution of oscillator energies which tends to zero in the high frequency limit. Thus Planck’s expression resolves ultraviolet catastrophe!
You can also express distribution of energy in terms of wavelength by making the subsittion \(\lambda = \frac{c}{\nu}\) obtaining:
The expressions for \(\rho_{\lambda}(T)d\lambda\) or \(\rho_{\nu}(T)d\nu\) have units of energy per volume which is why they are often referred as energy density of radiation. By integrating over the entire spectrum (e.g all wavelengths) one can obtain the total energy of radiation per volume!
In some books you may also find black body radiation characterized via the radiation flux which is a radiation measured per unit wavelength and per unit solid angle \(B_{\lambda} = \frac{c}{4\pi} \cdot \rho_{\lambda}\)
Wien’s displacement law#
The energy density peaks at a wavelength \(\lambda_{max} \) which is inversely proportional to the temperature. This relationship is described by Wien’s displacement law:
Where \( b \) is Wien’s displacement constant, approximately equal to \(2.8977729 \cdot 10^{-3} \) m·K.